But it was not the animals’ falls from dizzying heights that first puzzled physicists in the late 19th century. Instead experts were stumped by photographs of cats spinning on their own axis while falling and then landing on their feet. Images from that time show a person holding a cat by its legs so that its back is facing the ground. Then the animal is released. At first, the feline floats upside down in the air with its back facing the ground. But in the next shots, something happens that seems to defy the laws of physics: the cat turns and lands on its paws.
Of course, people knew from everyday observations that these quadrupeds can turn in the air. But it had been assumed that they obtain the momentum necessary for this movement by pushing off from the surface from which they fall. That’s because according to the conservation of angular momentum, it is impossible for an object that is not spinning to suddenly rotate without external influence. Yet that is exactly what the photographs show. Initially the cat falls straight down. Then it manages to rotate on its own axis. How is that possible?
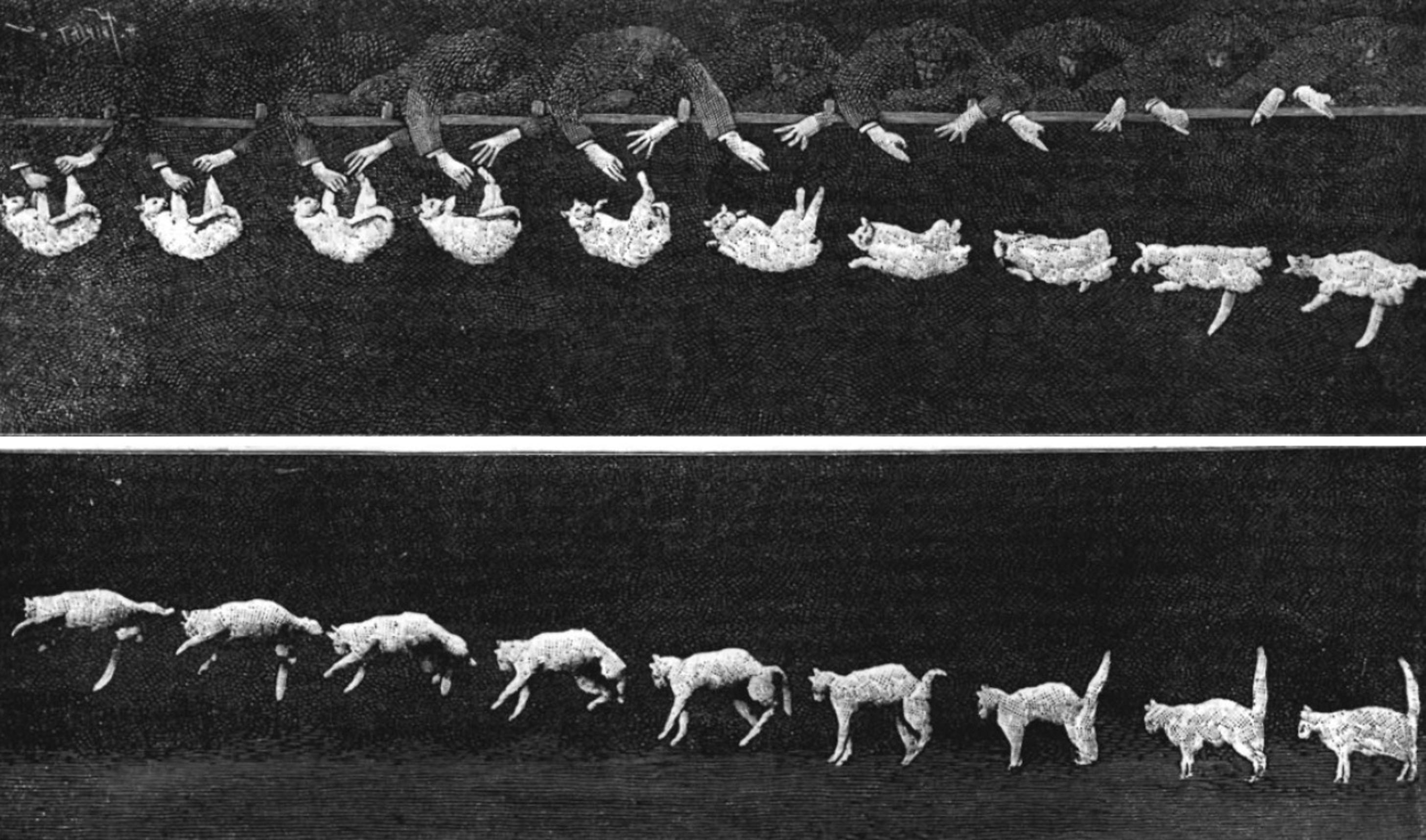
This phenomenon occupied many scientists, including physicist James Clerk Maxwell, known for his work on electromagnetism. He conducted several experiments in which he dropped cats from various heights (including from open windows) and onto beds and tables. But it wasn’t until 1969 that the “falling cat problem” was solved. As it turned out, the cat’s body had not been considered carefully enough. It is not simply a cylindrical object that magically begins to spin. If you look closely, you can see that a cat’s upper and lower body rotate in opposite directions. Thus, conservation of angular momentum is preserved. If the animal rotates like a pepper mill in two different directions, the change in angular momentum is zero.
But how does a cat manage to land on its paws? To do this, felines exploit the physical laws of classical mechanics: by placing their front paws close to their body, they reduce their moment of inertia. Like figure skaters, their upper body rotates quickly around its own axis. With their hind legs, the animals then employ the opposite effect. They stretch their legs to create as large a moment of inertia as possible. As a result, the upper body rotates through a large angle, while the legs rotate less in the opposite direction. The animals’ extremely flexible spine makes this movement possible. Once the upper body is now in the correct position (i.e., head aligned upright above the ground), cats can extend their front paws, tighten their hind legs and perform the pepper-mill-like movement in the opposite direction so that their hind paws are also aligned above the ground. In this way, the animals always manage to land on all fours—following all the laws of physics.
How High Can Cats Fall and Survive?
The laws of physics state that the higher the fall, the harder the impact. But a study from the 1980s paints a different picture—at least for cats. Two New York City veterinarians described a total of 132 cases between June and November 1984 in which cats had fallen from as high as the 32nd floor of high-rise buildings. Overall, 90 percent of the cats survived. When the veterinarians documented the injuries, they made an astonishing observation: while the severity of the damage increased up to a height of about seven stories, it seemed to decrease thereafter. In other words, a fall from the 11th floor could end more gently for a cat than one from the sixth floor.
Once again, the felines seemed to break the laws of physics. The higher the floor from which a body falls, the longer it is accelerated by Earth’s gravity. Thus, its speed should increase more and more until it finally hits the ground. The abrupt impact converts the animal’s kinetic energy from falling into other forms of energy, which can lead to broken bones, collapsed lungs, and worse. Thus, falling from high floors should have more unpleasant consequences than from low floors.
But this way of thinking about the feline free-fall ignores air resistance. After all, cats do not fall to the ground in a vacuum but move through air that can slow their fall. Thus, two opposing forces act on a cat during a fall: the gravitational force Fg and the frictional force FR, which slows it down. While Fg has a very simple form and is merely the product of the mass m of the cat and the acceleration caused by gravity g, the air resistance depends on the cross-sectional area A, the drag coefficient cW, the air density ρ and the velocity v of the falling object: FR = ½ x ρ x A x cW x v2. At the beginning of the fall, the cat has a velocity of zero, so only the acceleration caused by gravity acts on it, but as v increases, the opposite frictional force then makes itself felt. Thus, to determine the concrete motion of the animal, one must calculate the total force (Fg – FR). This then determines which acceleration acts on a cat of a certain weight m: m x a = Fg – FR.
A Speed Limit for Falling Felines
The acceleration corresponds to the change in velocity, which can be expressed mathematically by a derivative, a = d⁄dt v. So if you want to calculate the speed of the cat at a certain time, you have to solve a complicated system of equations containing both the speed itself and its derivative (acceleration): m x d⁄dtv = m x g −½ x ρ x A x cW x v2. For such differential equations, there is often no exact solution. In this case, it is possible to calculate a solution for the velocity corresponding to a hyperbolic tangent. Depending on the cross-section and weight of the cat, you end up with a curve that grows rapidly at the beginning and then flattens out and converges to a constant value: the animal gains speed quickly at the beginning of the fall before the air resistance eventually becomes so strong that it no longer speeds up, as physicist Rhett Allain of Southeastern Louisiana University calculated for Wired.
.png)
You can also calculate this terminal velocity, or upper speed limit, quite easily. Because the terminal velocity results when the frictional force is exactly as large as the gravitational force in this case, the two forces cancel each other out and a falling object plummets towards the ground with constant velocity. So you just have to solve the equation m x g = ½ ρ A cW v2 for v, and you get: v = √(2mg⁄ρAc).
To give a specific value for the terminal velocity of a cat, one need only insert numerical values for the variables. While one can estimate the weight and cross-sectional area of a cat, the drag coefficient is more difficult to determine. Suppose a cat weighs 4 kilograms (about 8.8 pounds), is 50 centimeters (around 19 inches) long and 15 centimeters (nearly 6 inches) wide. These measurements would give the animal a cross-sectional area of A = 0.075 square meters. The cat could also have the drag coefficient of a cylinder (cW = 0.8). Then the final speed of the animal is: v = 32.68 meters per second, which corresponds to just under 120 kilometers (or 74.5 miles) per hour.
To find out at what height a cat reaches this terminal velocity, one can solve the differential equation and thus calculate the velocity at the time of impact as a function of the height of the fall.
.png)
As can be seen from the graph, cats already reach a speed of 30 meters per second at a fall height of 100 meters. Because cats have already been observed to survive falls from higher buildings (such as from the 32nd floor), they can theoretically survive an impact with the greatest possible terminal velocity of 120 kilometers per hour. Consequently, the animals could, in theory, survive a fall from any conceivable height.
Actual Effect or Survivorship Bias?
But this terminal velocity calculation does not explain the observations of the New York veterinarians: Why do cats seem to survive a fall from the seventh floor or higher better than from lower floors? One explanation involves the animals’ experience.
When a cat falls from a low height, it is weightless for a short time. Instinctively, therefore, it will extend its legs underneath it to land on all fours. At high fall heights, however, this strategy is not useful: aligned legs can lead to serious injury because the animal’s weight is distributed awkwardly. This difference may explain why the survival rate decreases with increasing height—at least up to the seventh floor. But at greater fall heights, the frictional force becomes noticeable during the fall. That’s why, the veterinarians speculate, the cat no longer has the sensation of falling. Thus, it can relax and will not stretch its legs. It lands more gently, with a more even weight distribution and, therefore, better chances of survival.
But there is also a simpler explanation for the observation—albeit a more depressing one for animal lovers. The veterinarians’ findings could reflect the so-called survivorship bias. If a cat falls from a high floor and dies instantly, the owner probably won’t bother to stop by a veterinary clinic. Therefore, the number of unreported deaths is probably higher than what has been recorded by medical professionals.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
ABOUT THE AUTHOR(S)

Manon Bischoff is a theoretical physicist and editor at Spektrum, a partner publication of Scientific American. Credit: Nick Higgins

